बराबर बंटवारा (कक्षा 2 - अध्‍याय 9)

जितनी बार आप नई किताबों को देखते हैं उतनी ही बार आप अपने सर के बालों को नोच सकते हैं, खतरा सिर्फ इतना है कि आपकी खोपड़ी गंजी हो जाएगी लेकिन इन किताबों में गलतियां खत्‍म होने का नाम न लेंगी। इसलिए बेहतर है इन किताबों को पढ़ते वक्‍त अपने हाथों को खुद के सिर से दो हाथ दूर ही रखें।

कक्षा 2 में 9 पन्‍नों का पाठ बराबर बंटवारा के नाम से बनाया गया है। लेखकगणों ने इस नाम का संधि विच्‍छेद किया और पाठ के पन्‍नों का गैर बराबर बंटवारा करके पहले दो पन्‍ने बराबर की अवधारणा के अभ्‍यास में होम कर दिए। यह बात ठीक है कि बराबर की अवधारणा पर काम किया जाना जरूरी है लेकिन वह काम तो जोड़ घटाव तथा गुणा से पहले कर लिया जाना चाहिए। उस काम को इतनी देर बाद करने का कोई तुक नहीं बनती। और फिर भाग के संदर्भ में बराबर का इस्‍तेमाल बंटवारा करने के संदर्भ में किया जाता है यानी ऐसा बंटवारा जो बराबर हो, अकेले बराबर का भाग के लिहाज से कोई मतलब नहीं बनता।

आपको यह भी लग सकता है कि लेखकों का एक मकसद बच्‍चों को निर्देश पढ़ कर समझने में काबिल बनने की काबिलियत का विकास करने की राह में रोड़े  अटकाना है इसलिए वे ऐसी भाषा का इस्‍तेमाल करते हैं जिसे पढ़ कर या सुन का समझना मुश्किल हो। जैसे,

‘’नीचे दी गई तालिका 1 व 2 में चित्रों को देखिए गिनिए एवं बराबर से बराबर को मिलाइए’’

‘’नीचे तालिका में माला एवं खुले मोतियों को गिनिए सामने वाली तालिका से बराबर अंकों से मिलान कीजिए’’

पहले निर्देश में ‘चित्रों’ को ‘बराबर’ से जानबूझ कर दूर रखा गया है ताकि बराबर शब्‍द को सुनते वक्‍त बच्‍चों के दिमाग में उसका कोई मतलब न बन पाए। एक ही वाक्‍य में तीन निर्देश ठूंस दिए गए हैं। दूसरे निर्देश में गिनवा कर, बराबर अंकों से मिलान करने को कहा है। ये बराबर चीजें तो आपने सुनी होगी लेकिन ये बराबर अंक क्‍या होता है भई, इसे आप तलाश करते रहिए। दोनों वाक्‍यों की बुनावट तो आप देख ही रहे होंगे कि कैसी है। आप अफसोस ही जाहिर कर सकते हैं कि इन किताबों के लेखकों के लिए लिए एक वाक्‍य के निर्देश भी ठीक से लिख पाना इतना मुश्किल क्‍यों है, उन्‍होंने तो इसे लिख कर छोड़ दिया आखिरकार, इसे भुगतना तो बच्‍चों को ही है। 

अब हम अवधारणा सिखाने के तरीके पर आते हैं। पेज क्रमांक 63 पर बराबर बांट कर भाग करना सिखाने के लिए कार्टून विधि का इस्‍तेमाल किया गया है जिसमें अध्‍यापिका व बच्‍चों के चेहरे के चित्र तथा उनकी कही गई बातों को बुलबुलों में दिखाया गया है। अवधारणा का परिचय देने में तीन पन्‍नों की पर्याप्‍त जगह इस्‍तेमाल की गई है। आप खुश हो सकते हैं कि पहाड़े की मदद से भाग करने वाले पुराने तरीके से शुरूआत करने के बजाए ऐसा तरीका लिया गया है जिसमें बच्‍चों की रूचि भी हो और वे उसमें कुछ काम साथ साथ करके समझ भी पाएं। लेकिन पन्‍ने को देखने के बाद मिली खुशी, उसे पढ़ना शुरू करते ही काफूर होने लगती है।

भाग को सिखाने की शुरूआत में अध्‍यापिका अपने सामने पांच थालियां रख कर व उनमें तीन तीन लड्डू रख कर पूछती है – ‘’5 थालियां जिसमें 3-3 लड्डू हैं, तो बताइए कुल कितने लड्डू हैं।‘’ हरेक थाली के नीचे एक बच्‍चे का नाम लिखा है। एक लड़का गिन कर बताता है, -‘’बहन जी! 15 लड्डू हुए। एक लड़की बोलती है, ‘’सभी में बराबर बराबर तीन लड्डू हैं।‘’

अब आप अपने सर से दो तीन बाल नोचने से खुद को नहीं रोक सकते। अपने गुस्‍से पर थोड़ा काबू रखिए, अभी तो इसकी शुरूआत ही हुई है। इस पाठ का मकसद, बराबर बांट कर भाग सिखाना है या गुणा। अगर इस पाठ का मकसद बराबर बंटवारे की मदद से भाग सिखाना है तो शुरूआत गुणा व भाग के संबंधों से क्‍यों की जा रही है। मेरा ऐसा अनुमान है कि लेखकों ने संभवत: कहीं एक अच्‍छे विचार को सुना-पढ़ा होगा कि किसी भी नई अवधारणा को सिखाने से पहले उसे पूर्व ज्ञान से जोड़ना चाहिए। इस अच्‍छे विचार का एक सबूत वे आरंभ में ‘बंटवारे’ से तोड़ कर ‘बराबर’ की अवधारणा को सिखा कर दे चुके हैं। उससे भी उन्‍हें चैन नहीं पड़ा तो यहां उन्‍होंने यह सोच कर गुणा को ले लिया है कि चूंकि गुणा भाग से पहले सिखाया जाता है और दोनों का आपस में संबंध तो होता ही है इसलिए उसे भाग से पहले एक बार तरोजाता कर ही लेना चाहिए।

यह बात सही है कि गुणा व भाग का आपस में उलट संबंध है। लेकिन क्‍या इस संबंध का इस्‍तेमाल भाग सिखाने की शुरूआत में किया जाना चाहिए। क्‍या यह संबंध गुणा व भाग की समझ की बुनियाद बनने के बाद समझना आसान नहीं होता। क्‍या आप घटाव सिखाने की शुरूआत करते वक्‍त उसे जोड़ से उलट संबंध के तौर पर सिखाना आरंभ करते हैं। या घटाना अच्‍छी तरह से सिखाने के बाद जोड़ व घटाव, दोनों के संबंधों को सिखाते हैं। खैर इस पाठ में यह कोई पहली और आखरी समस्‍या तो है नहीं।

किताब में दी गई अब तक की बातचीत में किसी बच्‍चे का नाम नहीं लिया गया है ना ही पहले पन्‍ने के आखिर तक किसी का नाम लिया जाता है तो यह समझना थोड़ा मुश्किल हो जाता है कि थाली के नीचे बच्‍चों के नाम क्‍यों लिख दिए गए होंगे। इसी तरह लड़की द्वारा बोला गया वाक्‍य एक नकली वाक्‍य है और गैर जरूरी भी क्‍योंकि अध्‍यापिका ने तो यह बात पूछी ही नहीं। या तो आप यह बोलते हैं कि सभी में तीन तीन लड्डू हैं या फिर यह कि सभी में बराबर लड्डू है। वैसे भी गुणा का सवाल हल करने के बाद इस वाक्‍य को बोलने को कोई तुक नहीं। अगर आपकी निगाहें चित्र पर गई हों तो आप यह भी सोच सकते हैं कि क्‍या कोई थाली तीन लड्डुओं से पूरी भर जाती होगी।

अब अध्‍यापिका भाग सिखाने वाली बातचीत पर आती है। वह पूछती है, ‘’यदि इन्‍हीं लड्डुओं को तीन थालियों में बराबर बराबर भरना है तो कितने कितने लड्डू आएंगे ? लड़की जवाब देती है, बहन जी! तीनों में बराबर-बराबर 5-5 लड्डू आएंगे।‘’ आप देख सकते हैं कि यहां बराबर बंटवारे का दिखावा तो हुआ लेकिन बराबर बंटवारा हुआ ही नहीं।

इस पूरी बातचीत को समझने की कुंजी लड़की के जवाब में बोले गए बहन जी शब्‍द के बाद लगे विस्मयादिबोधक चिन्‍ह में है। इससे आपको यह सुराग मिलता है कि भाग के सवाल का जवाब किसी प्रक्रिया से नहीं बल्कि एक किस्‍म के इलहाम से मिलता है।

इस बातचीत को विस्‍तार से समझने की जरूरत है। पूरे पन्‍ने पर कहीं भी लड्डुओं का वह समूह नहीं है, जिसे बराबर बांटा जाना है। कहां है 15 लड्डुओं की ढेरी। या तो पहले सवाल में तीन तीन लड्डू की थाली का चित्र है या दूसरे सवाल में पांच पांच लड्डू की थाली का चित्र। आप खोजेंगे तो बड़ी मुश्किल से लड़के की बात में 15 का जिक्र मिल जाएगा और अध्‍यापिका के सवाल में उन लड्डुओं का संदर्भ मिल जाएगा लेकिन बगैर संख्‍या का नाम बोले। यानी लेखक गणों ने लड्डुओं को अदृश्‍य कर दिया है। कहीं उनहें यह डर तो नहीं सता रहा था कि आरंभ में 15 लड्डुओं के चित्र देने से बच्‍चे कहीं गलती से भी उन लड्डुओं की ढेरी को गिन कर उसका मतलब न समझ लें।

फिर भी, यह तो इस संवाद की आंरभिक अड़चन है। इस संवाद में सबसे बड़ी समस्‍या यह है कि पहले सवाल आता है और उसके बाद शब्‍दों में जवाब भी आ जाता है। तो इसमें किसी को क्‍या एतराज होना चाहिए। एतराज यह है कि इस पूरे तामझाम में भाग की संक्रि‍या तो होती कहीं भी नहीं दिख रही जिसे समझाने के लिए चित्र बनवाए गए व बातचीत के इतने पापड़ बेले गए थे। जवाब देने वाली लड़की को कैसे पता चला कि तीनों में बराबर लड्डू आएंगे। चित्र से कहीं यह पता नहीं चलता कि अध्‍यापिका के सवाल का जवाब निकालने के तीन खाली थालियां लेनी पड़ती है फिर उनमें अपने पास मौजूद उन अदृश्य लड्डुओं की कल्‍पना करनी पड़ती है व अंत में उनमें से एक एक को प्रकट करवा कर बांटना भी पड़ता है तब कहीं जाकर पता चलता है कि हरेक थाली में कितने कितने आएंगे और यह भी कि वे बराबर हैं या नहीं।

आप यह भी कह सकते हैं कि लड़की ने चित्र देख कर जवाब थोड़े ही दिया वह तो अध्‍यापिका की बात सुन कर जवाब दे रही है। तो सवाल उठ सकता है कि फिर थालियों में लड्डू दिखाने की जरूरत ही क्‍या थी। वैसे अगर चित्र देख कर वह जवाब देती तो यह कह सकती थी कि तीनों थालियों में 5 – 5 लड्डू हैं। लेकिन यहां पर एक नई मुश्किल यह भी है कि चित्र तो ऐसे हैं नहीं कि वह उन्‍हें देख कर व गिन कर बता पाए।

इस पन्‍ने से आप इस नतीजे पर पहुंच सकते हैं कि भाग का सवाल हल करने के लिए किसी किस्‍म का कोई काम करने की जरूरत नहीं है। सवाल सुनते ही आपके दिमाग में जवाब आ जाता है। और नहीं आए तो जवाब का न समझ आने लायक फोटो देख कर तो कैसा भी जवाब हो, आ ही जाता है। 

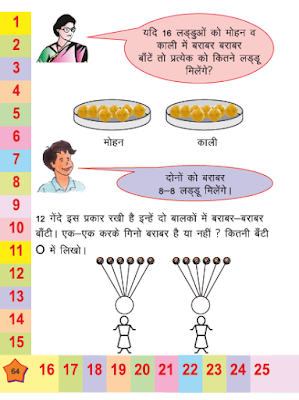इसी प्रगटीकरण या इलहाम की प्रक्रिया से अगले पन्‍ने पर दिए सवाल का जवाब चित्रित लड़के के दिमाग में रोशन हो जाता है।

इसके बाद लेखकों को लगा कि दो बार जवाबों का इलहाम करवाना तो काफी हो गया सो अब थोड़ा बहुत भाग की संक्रिया का दिखावा भी कर लिया जाए। चित्र बना कर किसी अवधारणा को सिखाना तो अच्‍छी बात मानी जाती है न। तो पेज क्रमांक 64 पर वे एक सवाल देते हैं जिसमें 12 गेंदों को 2 बच्चों में बांटना है। पन्‍ने की बची खुची जगह पर वे कांच की गोली के आकार की गेंदे बना कर उनके नीचे दो बच्‍चों के चित्र बना देते हैं। पहली छह गोलीनुमा गेंदों को पहले बच्‍चे तथा बाकी छह गोलीनुमा गेंदों को दूसरे बच्‍चे के सिर पर रखे गोले से जोड़ देते हैं। बच्‍चों को सिर्फ यह करना है कि छह गोलीनुमा गेंदों को गिने व उनसे जुड़े खाली गोले में लिख दें।

काम करवाया छह गेंदों को गिनवा कर लिखवाने का और दिखावा किया बराबर बांट कर भाग सिखाने का। अपने सिर के दो चार बाल और यह सोच कर नोच लीजिए कि दो पन्‍नों में लेखकों ने कितनी मेहनत की है छह गोलीनुमा गेंदों को गिनवाना सिखाने में। चलिए आपको याद दिला दूं कि 50 तक की संख्‍याएं तो बच्‍चा कक्षा 1 में ही गिनना सीख चुका होना चाहिए। आप थोड़ा चैन की सांस तो ले ही सकते है कि यहां तक आते आते बच्‍चे को कम से कम गिन कर लिखने के अभ्‍यास का मौका तो मिला। 

अब तक आपको यह समझ में आ ही गया होगा कि असली माजरा तो यह है कि लेखकगणों को चित्रों के जरिए बच्‍चों से बराबर बंटवारा करवा कर भाग सिखाना आता ही नहीं है। इसलिए वे कहीं भी सवाल को हल करने के लिए भाग की प्रक्रिया का इस्‍तेमाल नहीं करते। वे सवाल लेते हैं। उसका जवाब उन्‍हें पता है, इसलिए वे जादूगर की तरह अपनी दायीं या बायीं जेब से जवाब निकालते हैं और उसी जवाब को चित्र के जरिए दर्शा देते हैं और इस काम के जरिए उम्‍मीद यह करते हैं कि बच्‍चे भाग को बराबर बांटने की प्रक्रिया के तौर पर सीख जाएंगे। 

इसका सबूत अगले ही पेज क्रमांक 65 पर फिर से मिल जाता है, जब वे इन्‍हीं 12 गेंदों को(जो तस्‍वीर में गोली के आकार से बड़ी हो चुकी होती है) तीन बालकों में बंटवाने को चित्र में दर्शाते हैं। चित्र वाला बच्‍चा खुश होकर लेखकगणों की जेब से निकले जवाब को बोल देता है।

आप लेखकों की हिम्‍मत की दाद ही दे सकते हैं कि जो काम जिस तरीके से उन्‍हें तक करना नहीं आता, उसकी काम को करने के लिए वे तीसरे पन्‍ने पर बची खुची जगह का इस तरह इस्‍तेमाल करते हैं कि अगर कोई बच्‍चा खुद के बूते करना भी चाहे तो जगह की तंगी के चलते करने की सोच ही न सके। अफसोस यहां पर लेखकगणों की जेब से निकला जवाब मौजूद नहीं है। और भाग के सवाल का जवाब खोजने की प्रक्रिया लेखकों ने उसे इन तीन पन्‍नों में अब तक सिखाई ही नहीं। 

आप जैसे ही पेज क्रमांक 66 पर दिए गए अभ्‍यास पर आते हैं तो पहले ही सवाल से साफ हो जाता है कि लेखकों का मकसद तो पहाड़ों को बोल कर भाग करना सिखाना था। यहां पर भी दिखावे के लिए वस्‍तु, डिब्‍बों की संख्‍या तथा प्रत्‍येक में कितने कितने भरेंगे, यह पूछा गया है। लेकिन चूंकि किताब में चीजों की मदद से बराबर बांट कर हल करना सिखाया ही नहीं गया तो अध्‍यापक व बच्‍चों के पास एक ही बरसों से आजमाया हुआ रास्‍ता बचता है - पहाड़े बोल कर भाग के सवाल हल करने का। तो आप पहाड़े बुलवाइये और भाग सिखाइए क्‍यों इतना परेशान होते हैं बराबर बंटवारा करके भाग सिखाने की मशक्‍क्‍त करने में।लेखकगण रचनावाद से सिखाने का दिखावा करते करते पहाड़ों से भी भाग करने का परिचय  नहीं करवा पाते।

रवि कांत